Original page: http://www.math.stonybrook.edu/~tony/mazes/satmaze.html
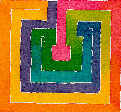
Sokkeloiden kautta matematiikkaan
Tunnetuin näistä sokkeloista on kreetalainen sokkelo. Se voidaan piirtää pelinä.
Tässä on toinen esimerkki. Tämä sokkelo esiintyy useissa keskiaikaisissa heprealaisissa käsikirjoituksissa. Vaikka tällä sokkelolla on pinnallinen samankaltaisuus Kreetan sokkeloon, läheinen vertailu osoittaa, että ne ovat melko erilaisia. Jerichon sokkelossa on 7 tasoa, kun taas Kreetan sokkelossa on 8, ja järjestys, jossa tasot saavutetaan, eroaa sokkelosta toiseen. Molemmissa sokkeloissa polku kulkee suoraan tasolle 3 (lasketaan ulkopuoli 0: ksi), mutta Kreetan sokkelossa se kaksinkertaistuu sitten takaisin tasojen 2 ja 1 kautta, kun taas Jerichon sokkelossa se jatkuu tasojen 4 ja 5 läpi ennen kuin palaa tasolle 2 ja 1. Täydelliset tasosekvenssit ovat
Kreetalainen 032147658
Jericho 03452167.
Ominaisuudet, joita nämä kaksi sokkeloa jakavat ja jotka auttavat määrittelemään sokkeloiden luokan yksinkertaisella matemaattisella kuvauksella, voidaan tiivistää kutsumalla niitä yksinkertaisiksi, vuorotellen, sokkeloiksi sokkeloiksi.
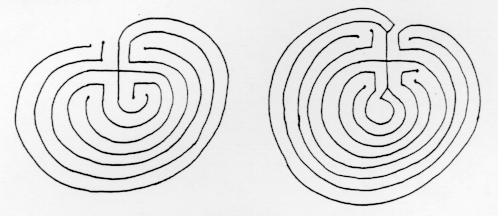KULKEVAT-sokkelot, koska polku kulkee ilman haarautumista sokkelon ulkopuolelta keskustaan. Esimerkiksi nämä sokkelot eivät ole kauttakulku labyrintteja: yhdessä polku tulee ulos samalla puolella kuin se tuli; ja toisessa on kohtia, joissa sokkelo-juoksijan on valittava kumpi tie mennä.
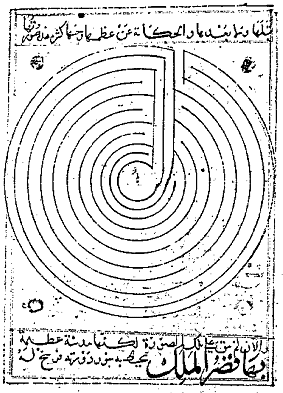VUOROTELLEN, koska sokkelon suunnitelma on asetettu tietylle määrälle samankeskisiä tai yhdensuuntaisia tasoja, ja sokkelon polku muuttaa suuntaa aina, kun se vaihtaa tasoa. Esimerkiksi tämä sokkelo, joka edustaa Konstantinopolin suunnitelmaa keskiaikaisessa arabialaisessa maantieteellisessä kirjassa, on erilliset tasot, mutta se ei ole vuorotteleva, koska se kiertyy tasolta 10 tasolle 1 muuttamatta suuntaa. Sen taso järjestyksessä 0.3.4.5.6.7.8.9.10.1.2.11 ei voi tapahtua, kuten tulemme näkemään, koska taso sekvenssi vaihtovirran sokkelo.
YKSINKERTAINEN, koska polku muodostaa olennaisesti täydellisen ympyrän kullakin tasolla; erityisesti se matkustaa kullakin tasolla täsmälleen kerran. Esimerkiksi tämä vuorotteleva labyrintti, joka esiintyy jalkakäytävän sokkelona Chartresissa (esitetty tässä) ja useissa muissa katedraaleissa ja veistetty pylvääseen Luccan katedraalissa, ei ole yksinkertainen: polkua on neljä eri kohtaa voi muuttaa tasoja. Tämä sokkelomalli näyttää tapahtuneen kreetalaisen suunnittelun ja sen roomalaisten jälkeläisten kristillisenä kehityksenä ja vahvistuksena; yhteys Theseus-myyttiin jatkui. Uusi muotoilu oli itsessään erittäin pysyvä. Se näkyy keskiaikaisissa käsikirjoituksissa, jotka ovat peräisin 9. vuosisadalta; Chartresin katedraali rakennettiin noin vuonna 1200; ja 1500-luvun alussa identtinen kuvio on maalattu florentiinille kasoni. Se on nyt renderöity kolmiulotteisesti panssaroidun Theseuksen taistellessa Minotauruksen keskellä.
TOPOLOGIA on yksinkertainen, vuorotteleva kauttakulku sokkelo määrää täysin sen taso sekvenssi.
Tony Phillips
Matematiikan osasto SUNY Stony Brook
tony at math.stonybrook.edu
30. syyskuuta 2020