Original page: http://www.cs.cmu.edu/~bryant/boolean/maps.html
Don Knuth työskentelee Tilavuus 4 Tietokoneohjelmoinnin taide. Yksi luvuista on Binääri päätös kaaviot ja niiden sovellukset, aihe, joka mielestäni erittäin mielenkiintoinen. Knuth osoittaa, että monia mielenkiintoisia kuvaaja ongelmat voidaan koodata Boolen kaavoja, ja johdettu BDD edustaa kaikkia mahdollisia ratkaisuja tähän ongelmaan. Usein on jonkinlainen optimointikriteeriksi, ja se on melko helppo poimia ”paras” ratkaisu BDD yksinkertaisella dynaaminen ohjelmointi algoritmi.
Tässä näytämme muutamia esimerkkejä käyttäen kuviossa esitetään 48 yhtenäiseen jäsenvaltioiden, jossa solmun kunkin valtion ja reuna kahden valtiota, jos ne on yhteinen raja. Kullekin karttojen, jos klikkaat hän kuvaa tulet lähdedokumentin SVG-muodossa. Tässä on kaavio, paikallistamiseen imusolmukkeita pääkaupungeissa valtioiden:

Pääkaupunkitorni
Oletetaan, että haluat käydä 48 osavaltion pääkaupunki vaatimusta, että olet vain läpi kunkin valtion kerran. (Toisin sanoen, haluat löytää Hamiltonin polku kaaviossa.) Kuten voitte nähdä edellä kartan, jos noudatat suorin reitti osavaltioiden pääkaupungit, sinun tulee usein läpi toisen valtion tai jos kyseessä on menee Lansing Madison, Wisconsin, voit ajaa koko Michigan-järvi. Sen sijaan, sinun pitäisi ottaa lyhin ajoreitti, joka pysyy sisällä kahden valtion jokaisen matkan osaa. Kutsukaamme tällaista reitille Pääkaupunkitorni. Tässä on kaavio sallitun reiteillä valtioiden:

Yksinkertaisen analyysin ja Knuthin ponnistelujen perusteella voimme sanoa:
- Kaikkien retkien on aloitettava tai päättynyt Maine, koska Maine on vain yksi naapuri. Käytämme Maineä lähtökohtana.
- Kaikkien retkien täytyy päättyä New Yorkin ulkopuolelle, koska se on nivelpiste.
- Yhteensä 68 686 026 eri pääkaupunkia.
Tässä on lyhin pääkauppa, yhteensä 11 698 mailia:

Tässä on pisin pääkaupunkierros, yhteensä 18 040 mailia:

Kaavio värjäys
Toinen mielenkiintoinen luokka ongelmista liittyy väritys kartan. Sääntö on, ettei kaksi vierekkäistä valtiot voivat olla samanvärisiä. Kuuluisa neliväriongelma todetaan tassun kuvaaja voi värjätä enintään neljä väriä.
Koska BDD koodaa kaikki mahdolliset ratkaisut Boolen kaavaan, voimme helposti laskea kuinka monta ratkaisua on. Kaavion värjäyksessä säädämme lukumme symmetrian poistamiseksi, koska väriarvot ovat mielivaltaisia (4! Symmetriset kotelot 4-väritykselle).
48 vierekkäisen tilan värjäämisessä on 533 816 322 048 mahdollista väriä. (Tämä on 1/2 Knutin ilmoittamaa numeroa, koska hänen karttansa sisältää Washingtonin DC: n 49. “tilana”, ja se voidaan määrittää jommallakummalle väristä, joita ei käytetä Marylandiin ja Virginiaan.) Tässä on muutamia mielenkiintoisia esimerkkejä erikoisvärit:
- Tasapainoinen väri, jossa kutakin väriä käytetään tarkalleen 12 tilaan. Tällaisia värejä on 12 554 677 864, mikä on yllättävän korkea 2,4% kaikista mahdollisista värityksistä.
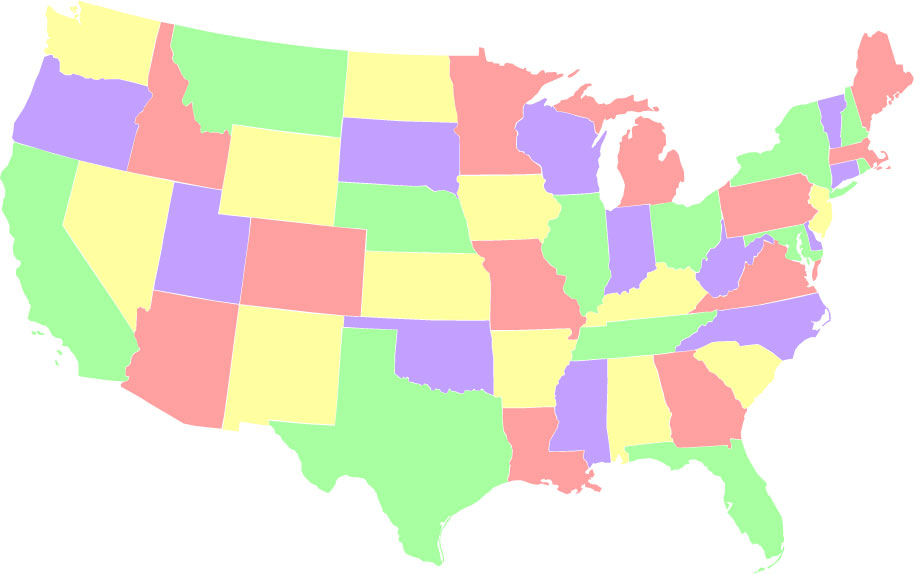
- Epätasapainoinen väritys, jossa yhtä väriä (vihreä) käytetään mahdollisimman vähän (2 tilaa). On vain 288 tapaa värittää kartta niin, että yksi väri käytetään vain kahdesti.

- Epätasapainoinen väritys, jossa yhtä väriä (keltainen) käytetään mahdollisimman paljon (18 tilaa). Kartalla on 71 002 368 tapaa värin värittämiseen siten, että yhtä väriä käytetään 18 kertaa.
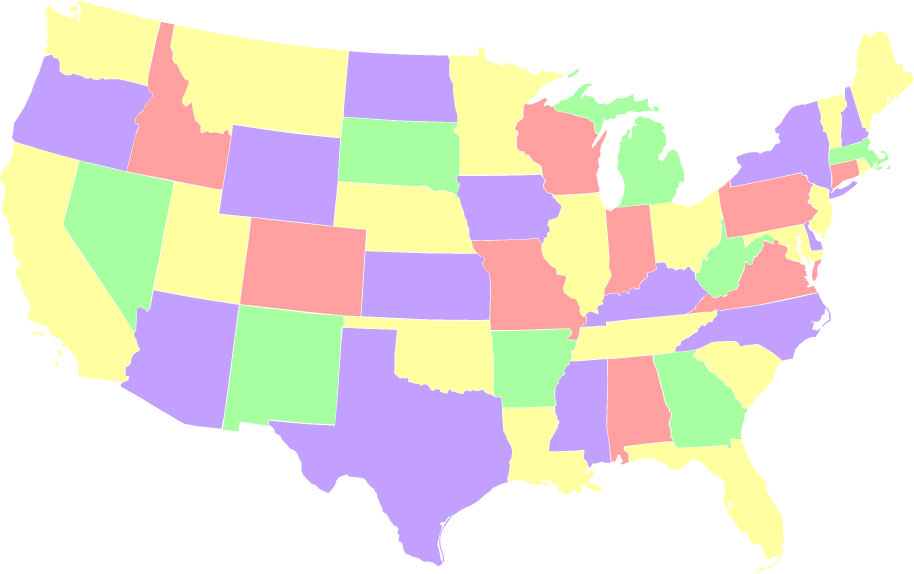
- Molempien yhdistäminen. Värit 2, 13, 15 ja 18 kertaa. Tämä sekvenssi 1) vasemmalta oikealle, käyttää kutakin väriä peräkkäin mahdollisimman vähän kertaa ja 2) oikealta vasemmalle, käyttää kutakin väriä peräkkäin mahdollisimman monta kertaa. Tällaisia ratkaisuja on 24.

Näkökulmasta kaavio värjäys ohjelmien kartta Yhdysvaltain 48 osavaltiossa on melko yksinkertainen. Saat haastavampaa karttaa, katso www-sivun McGregor kaavio.
