Original page: http://staff.um.edu.mt/jskl1/dp/th.html

Jaroslav Sklenar, 30. lokakuuta 2007

Esittely

Hanoin tornit on tunnettu peli (palapeli), jota käytetään tyypillisesti selittämään ja osoittamaan rekursion voimakkuus. On hyvin monia verkkosivustoja, jotka käsittelevät sitä. Mainitakseni joitain monista, voit käydä esimerkiksi:

http://en.wikipedia.org/wiki/Tower_of_Hanoi

http://hanoitower.mkolar.org/

http://www.cut-the-knot.org/recurrence/hanoi.shtml

http://mathworld.wolfram.com/TowerofHanoi.html

ja monet muut. Ongelmaa voidaan käyttää myös osoittamaan dynaamisen ohjelmoinnin tehokkuutta. Lisätietoja lukea paperin Moshe Sniedovich on http://archive.ite.journal.informs.org/Vol3No1/Sniedovich/ jossa Dynaaminen ohjelmointi on käytetty löytämään pituus lyhin liuosta ja myös pituus lähes huomiotta pisin ratkaisu (ja paljon muuta). Täällä käytämme Dynaaminen ohjelmointi lähestymistapa löytää useita eri ratkaisuja.

Olen saavuttanut tuloksen itse, mutta luulen, että en ole ensimmäinen. Kerro minulle viittaukset lähteeseen, jossa tämä kaava on julkaistu. Minulla on ilo mainita se.

Teoria

Oletan tässä, että lukija tuntee ongelman, joten vain lyhyt yhteenveto:

Kolme alustat (pylväät) kutsutaan L (vasen), C (keski) ja R (oikea). 

Torni on kokoelma levyjä (renkaat) päällekkäin muiden siten, että aina pienempi levy asetetaan isompi. Aluksi torni korkeus n tehty levyjen 1…n kasvavalla koolla, jossa 1 on suurin pienin levy, joka sijaitsee alustan L.

Säännöt: levyjä siirtäessä meidän on noudatettava seuraavia sääntöjä:

– vain yhtä levyä kerrallaan voidaan siirtää

– levy voidaan asettaa joko tyhjälle alustalle tai isommalle levylle.

Ongelma: haluamme siirtää levyistä 1…n tehdyn tornin laiturilta L tasolle R noudattamalla sääntöjä.

Pelin tilan antaa kolme toisiaan poissulkevaa sarjaa  sellainen, että . Mahdollinen tila on sellainen, johon päästään noudattamalla sääntöjä. Tämä takaa myös sen, että nämä sarjat ovat joko torneja tai ne voivat olla tyhjiä. Alkuperäinen tila on , lopullinen tila on .

Ratkaisu on siirtojen sarja (vaihtoehtoisesti näiden siirtojen muodostama tilajärjestys), joka ratkaisee yllä olevan ongelman noudattamalla sääntöjä. Tarkastelemme vain sellaisia ratkaisuja, joissa ei ole jaksoja, joissa kukin tila esiintyy enimmäkseen kerran.

Olkoon F(n,a,b,c) erilaisten ratkaisujen kokonaismäärä ongelmaan, joka liittyy n korkeuden tornin siirtämiseen laiturilta a lavalle b käyttämällä laitetta c. Koska alustojen välillä ei ole eroa sääntöjen suhteen, voimme käyttää F(n) ta lyhyeksi.

Lause: F(n) voidaan laskea rekursiivisella kaavalla

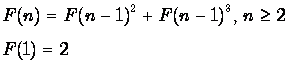
Todiste: Varten n = 1 on selvästi kaksi ratkaisua ilman jaksoja: siirrä levy L: stä R: hen tai siirrä levy L: stä C: een ja sitten C: stä R. Nyt oletamme . Lopputilan saavuttamiseksi suurin levy n on siirrettävä L: stä R. Tämä voidaan tehdä (aina ilman jaksoja) kahdella eri tavalla, joita käsittelemme erikseen.

1)  Siirrä torni (n-1) alkaen L ja C, siirrä levyä n alkaen L ja R, siirrä torni (n-1) alkaen C ja R. Tornin siirtäminen (n-1) alkaen L ja C on F(n-1) erilaisia ratkaisuja, tornin siirtäminen (n-1) alkaen C ja R on myös F(n-1) erilaisia ratkaisuja. Nämä korkeustornien kaksi liikettä (n-1) ovat riippumattomia, joten ensimmäinen tapaus johtaa F(n-1)² erilaisia ratkaisuja.

2)  Siirrä torni (n-1) alkaen L ja R, siirrä levyä n alkaen L ja C, siirrä torni (n-1) alkaen R ja L, siirrä levyä n alkaen C ja R, siirrä torni (n-1) alkaen L ja R. Näemme, että tornissa on kolme itsenäistä liikettä (n-1), joten eri ratkaisujen kokonaismäärä tässä tapauksessa on F(n-1)³.

Koska tapaukset 1) ja 2) sulkevat toisiaan pois, meillä on lausekaavan antama eri ratkaisujen kokonaismäärä. ÿ

Legendoja

On legenda, joka keksittiin todennäköisesti tyhjästä yhdessä pelin kanssa vuonna 1883, jonka ranskalainen matemaatikko Edouard Lucas:

”Legendan mukaan joukko itäisiä munkkeja pitää yllä kolmea tornia, joilla istuu 64 kultaista rengasta. Alun perin kaikki 64 rengasta oli pinottu yhteen torniin jokaisen renkaan ollessa pienempi kuin alla oleva. Munkkien on siirrettävä renkaat ensimmäisestä tornista kolmanteen torniin kerrallaan, mutta ei koskaan siirrä suurempaa rengasta pienemmän päälle. Kun kaikki 64 rengasta on siirretty, maailma loppuu”.

(Lisätietoja katso sivun http://hanoitower.mkolar.org josta legendan otettiin).

On hyvin tiedossa, että optimaalinen ratkaisu n tornien peliin vie 2ⁿ-1 siirtoa. Jos oletetaan, että yksi siirto vie yhden sekunnin, saavutamme yksinkertaisen laskelman jälkeen tuloksen, johon ratkaisu sopii n = 64 kestää noin 585×10⁹ vuotta.

Voimme tarjota toisen legendan:

”Ota vain 5 rengasta ja kokeile kaikkia mahdollisia ratkaisuja. Sitten maailmankaikkeus loppuu”.

Jos otamme (epärealistisen) oletuksen, että jokainen ratkaisu kestää keskimäärin (niiden pituus on erilainen) vain yhden sekunnin, kaikkien kokeileminen vie noin 89.67×10²⁰ vuotta. Tarpeeksi aikaa monille isoille otsatupeille.

Vielä yksi legenda:

“Ota vain 4 rengasta ja anna jokaisen ihmisen maapallolla ratkaista peli eri tavalla. Kun kaikkia erilaisia ratkaisuja käytetään, maailmankaikkeus loppuu”.

Aikaisemmin maailmankaikkeuden lopussa ei ollut ollenkaan, mutta nyt tämä on muuttunut. Silti meillä on melkein yksi ratkaisu jokaiselle ihmiselle.

Tulokset

Nämä ovat lukuisia ratkaisuja tornikorkeuden lisäämiseen:

F(1) = 2

F(2) = 12

F(3) =  1872

F(4) =  6,563,711,232

F(5) ≈  2.827798101718050e+029

Seuraavassa on kaikki ratkaisut korkeuden 1,2 ja 3 torneihin (ote). Jokainen rivi sisältää yhden ratkaisun, joka alkaa sen numerosta. Välilyönnillä erotetut siirrot ovat muodossa:

kAB

missä k on levyn numero, jonka siirrymme tasolta A tasolle B. Huomaa, että ensimmäinen ratkaisu on lyhin, jossa 2ⁿ-1 siirtää, viimeinen ratkaisu on pisin 3ⁿ-1 siirtolla.

    1 (tornin korkeus)

    2 (luotujen ratkaisujen lukumäärä)

    1 1LR

    2 1LC 1CR

 

    2 (tornin korkeus)

   12 (luotujen ratkaisujen lukumäärä)

    1 1LC 2LR 1CR

    2 1LC 2LR 1CL 1LR

    3 1LR 1RC 2LR 1CR

    4 1LR 1RC 2LR 1CL 1LR

    5 1LR 2LC 1RL 2CR 1LR

    6 1LR 2LC 1RL 2CR 1LC 1CR

    7 1LR 2LC 1RC 1CL 2CR 1LR

    8 1LR 2LC 1RC 1CL 2CR 1LC 1CR

    9 1LC 1CR 2LC 1RL 2CR 1LR

   10 1LC 1CR 2LC 1RL 2CR 1LC 1CR

   11 1LC 1CR 2LC 1RC 1CL 2CR 1LR

   12 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR

    3 (tornin korkeus)

 1872 (luotujen ratkaisujen lukumäärä)

    1 1LR 2LC 1RC 3LR 1CL 2CR 1LR

    2 1LR 2LC 1RC 3LR 1CL 2CR 1LC 1CR

    3 1LR 2LC 1RC 3LR 1CR 1RL 2CR 1LR

    4 1LR 2LC 1RC 3LR 1CR 1RL 2CR 1LC 1CR

    5 1LR 2LC 1RC 3LR 1CR 2CL 1RC 2LR 1CR

    6 1LR 2LC 1RC 3LR 1CR 2CL 1RC 2LR 1CL 1LR

    7 1LR 2LC 1RC 3LR 1CR 2CL 1RL 1LC 2LR 1CR

    8 1LR 2LC 1RC 3LR 1CR 2CL 1RL 1LC 2LR 1CL 1LR

    9 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RC 2LR 1CR

   10 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RC 2LR 1CL 1LR

   11 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RL 1LC 2LR 1CR

   12 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RL 1LC 2LR 1CL 1LR

   13 1LR 2LC 1RL 1LC 3LR 1CL 2CR 1LR

   14 1LR 2LC 1RL 1LC 3LR 1CL 2CR 1LC 1CR

   15 1LR 2LC 1RL 1LC 3LR 1CR 1RL 2CR 1LR

   16 1LR 2LC 1RL 1LC 3LR 1CR 1RL 2CR 1LC 1CR

   17 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RC 2LR 1CR

   18 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RC 2LR 1CL 1LR

   19 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RL 1LC 2LR 1CR

   20 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RL 1LC 2LR 1CL 1LR

      . . .

 1865 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

           3CR 1LR 2LC 1RL 2CR 1LR

 1866 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

           3CR 1LR 2LC 1RL 2CR 1LC 1CR

 1867 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

           3CR 1LR 2LC 1RC 1CL 2CR 1LR

 1868 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

           3CR 1LR 2LC 1RC 1CL 2CR 1LC 1CR

 1869 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

           3CR 1LC 1CR 2LC 1RL 2CR 1LR

 1870 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

      3CR 1LC 1CR 2LC 1RL 2CR 1LC 1CR

 1871 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

          3CR 1LC 1CR 2LC 1RC 1CL 2CR 1LR

 1872 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL

          3CR 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR

Voit ladata tekstitiedosto kaikki ratkaisuja varten tornin korkeus 3.

Eri ratkaisujen määrä pienillekin tornille on vaikuttava. Jos haluat tarkistaa kaavan, jonka olen kirjoittanut Turbo Pascal 7 ohjelmiin, jotka tuottavat ratkaisut tekstitiedostoon yllä olevassa muodossa, tarkista ovatko ratkaisut kaikki erilaisia ja simuloi niitä tarkistaaksesi, ovatko ne oikeita. Niitä voidaan käyttää myös käsin luotuihin ratkaisuihin. Jos haluat voit ladata nämä ohjelmat. Kaikki tulisi selvitä kommentit lähdetiedostot.